logica matematica
Proposiciones:
Llamaremos de esta forma a cualquier afirmación que sea verdadera o falsa, pero no ambas cosas a la vez.
Ejemplo
1. Las siguientes afirmaciones son proposiciones.
(a) Gabriel García Marqués escribió Cien años de soledad.
(b) 6 es un numero primo. }
(c) 3+2=6
(d) 1 es un numero entero, pero 2 no lo es.
Nota 1.1 Las proposiciones se notan con letras minúsculas, p, q, r . . . . . . La notación p :Tres mas cuatro es igual a siete se utiliza para definir que p es la proposición “tres mas cuatro es igual a siete”. Este tipo de proposiciones se llaman simples, ya que no pueden descomponerse en otras.
Ejemplo
2. Las siguientes no son proposiciones.
(a) x + y > 5
(b) ¿Te vas?
(c) Compra cinco azules y cuatro rojas.
(d) x = 2
Solución En efecto, (a) es una afirmación pero no es una proposición ya que sera verdadera o falsa dependiendo de los valores de x e y e igual ocurre con la afirmación (d). Los ejemplos (b) y (c) no son afirmaciones, por lo tanto no son proposiciones. Desde el punto de vista lógico carece de importancia cual sea el contenido material de los enunciados, solamente interesa su valor de verdad.
Clases:
*Proposición Compuesta
Si las proposiciones simples p1, p2, . . . , pn se combinan para formar la proposición P, diremos que P la es una proposición compuesta de p1, p2, . . . , pn.
Ejemplo
“La Matemática Discreta es mi asignatura preferida y Mozart fue un gran compositor” es una proposición compuesta por las proposiciones “La Matemática Discreta es mi asignatura preferida” y “Mozart fue un gran compositor”.
“El es inteligente o estudia todos los días” es una proposición compuesta por dos proposiciones: “El es inteligente” y “El estudia todos los días”.
Conexión entre Proposiciones
Estudiamos en este apartado las distintas formas de conectar proposiciones entre sı. Prestaremos especial atención a las tablas de verdad de las proposiciones compuestas que pueden formarse utilizando las distintas conexiones.
Conjunción
Dadas dos proposiciones cualesquiera p y q, llamaremos conjunción de ambas a la proposición compuesta “p y q” y la notaremos p ∧ q. Esta proposicion ser´a verdadera únicamente en el caso de que ambas proposiciones lo sean.
Observe se que de la definicion dada se sigue directamente que si p y q son, ambas, verdaderas entonces p ∧ q es verdad y que si al menos una de las dos es falsa, entonces p ∧ q es falsa. Por lo tanto su tabla de verdad vendrá dada por
Disyunción Dadas dos proposiciones cualesquiera p y q, llamaremos disyunción de ambas a la proposición compuesta “p ´o q” y la notaremos p ∨ q. Esta proposición sera verdadera si al menos una de las dos p o q lo es. De acuerdo con la definicion dada se sigue que si una de las dos, p o q, es verdad entonces p∨q es verdad y que p ∨ q sera falsa, únicamente si ambas lo son. Su tabla de verdad sera, por tanto.
Cuando se habla de cuantificadores en términos de Lógica, Teoría de Conjuntos o Matemáticas en general, se hace referencia a aquellos símbolos que se utilizan para indicar cantidad en una proposición, es decir, permiten establecer “cuántos” elementos de un conjunto determinado, cumplen con cierta propiedad.
Los cuantificadores permiten la construcción de proposiciones a partir de funciones proposicionales, bien sea particularizando o generalizando. Por ejemplo, si consideramos la función proposicional:
P(x) = x es menor que dos
Esto podría particularizarse así: “Existe un número real que es menor que dos” o generalizarlo diciendo: “Todos los números reales son menores que dos”.
En cualquiera de los dos casos, se especifica un conjunto donde está tomando valores la variable, para nuestro ejemplo, el conjunto de los números reales.
Para notar la particularización y la generalización, se utiliza la siguiente simbología, respectivamente:

que se lee: “existe un equis que pertenece a erre (a los reales), tal que equis es menor que dos”
Mientras que

se lee: “para todo equis que pertenece a erre (a los reales), se cumple que equis es menor que dos”
El símbolo (para todo…) se denomina cuantificador universal, y el símbolo
(para todo…) se denomina cuantificador universal, y el símbolo  (existe al menos un…) se denomina cuantificador existencial.
(existe al menos un…) se denomina cuantificador existencial.
Así, un cuantificador transforma una función proposicional, en una proposición a la cual se le asigna un valor de verdad.
Los cuantificadores más utilizados son entonces:



NEGACIÓN DE PROPOSICIONES CON CUANTIFICADORES
Sea p(x) una función proposicional con extensión A, entonces:


Llamaremos de esta forma a cualquier afirmación que sea verdadera o falsa, pero no ambas cosas a la vez.
Ejemplo
1. Las siguientes afirmaciones son proposiciones.
(a) Gabriel García Marqués escribió Cien años de soledad.
(b) 6 es un numero primo. }
(c) 3+2=6
(d) 1 es un numero entero, pero 2 no lo es.
Nota 1.1 Las proposiciones se notan con letras minúsculas, p, q, r . . . . . . La notación p :Tres mas cuatro es igual a siete se utiliza para definir que p es la proposición “tres mas cuatro es igual a siete”. Este tipo de proposiciones se llaman simples, ya que no pueden descomponerse en otras.
Ejemplo
2. Las siguientes no son proposiciones.
(a) x + y > 5
(b) ¿Te vas?
(c) Compra cinco azules y cuatro rojas.
(d) x = 2
Solución En efecto, (a) es una afirmación pero no es una proposición ya que sera verdadera o falsa dependiendo de los valores de x e y e igual ocurre con la afirmación (d). Los ejemplos (b) y (c) no son afirmaciones, por lo tanto no son proposiciones. Desde el punto de vista lógico carece de importancia cual sea el contenido material de los enunciados, solamente interesa su valor de verdad.
Clases:
*Proposición Compuesta
Si las proposiciones simples p1, p2, . . . , pn se combinan para formar la proposición P, diremos que P la es una proposición compuesta de p1, p2, . . . , pn.
Ejemplo
“La Matemática Discreta es mi asignatura preferida y Mozart fue un gran compositor” es una proposición compuesta por las proposiciones “La Matemática Discreta es mi asignatura preferida” y “Mozart fue un gran compositor”.
“El es inteligente o estudia todos los días” es una proposición compuesta por dos proposiciones: “El es inteligente” y “El estudia todos los días”.
Conexión entre Proposiciones
Estudiamos en este apartado las distintas formas de conectar proposiciones entre sı. Prestaremos especial atención a las tablas de verdad de las proposiciones compuestas que pueden formarse utilizando las distintas conexiones.
Conjunción
Dadas dos proposiciones cualesquiera p y q, llamaremos conjunción de ambas a la proposición compuesta “p y q” y la notaremos p ∧ q. Esta proposicion ser´a verdadera únicamente en el caso de que ambas proposiciones lo sean.
Observe se que de la definicion dada se sigue directamente que si p y q son, ambas, verdaderas entonces p ∧ q es verdad y que si al menos una de las dos es falsa, entonces p ∧ q es falsa. Por lo tanto su tabla de verdad vendrá dada por
Disyunción Dadas dos proposiciones cualesquiera p y q, llamaremos disyunción de ambas a la proposición compuesta “p ´o q” y la notaremos p ∨ q. Esta proposición sera verdadera si al menos una de las dos p o q lo es. De acuerdo con la definicion dada se sigue que si una de las dos, p o q, es verdad entonces p∨q es verdad y que p ∨ q sera falsa, únicamente si ambas lo son. Su tabla de verdad sera, por tanto.
Disyunción Exclusiva
Dadas dos proposiciones cualesquiera p y q, llamaremos disyunción exclusiva de ambas a la proposición
compuesta “p o q pero no ambos” y la notaremos p Y q. Esta proposición sera verdadera si una u otra,
pero no ambas son verdaderas.
Según esta definicion una disyunción exclusiva de dos proposiciones p y q ser´a verdadera cuando tengan
distintos valores de verdad y falsa cuando sus valores de verdad sean iguales.
Disyunción:
Dadas dos proposiciones cualesquiera p y q, llamaremos disyunción de ambas a la proposición compuesta
“p o q” y la notaremos p ∨ q. Esta proposición sera verdadera si al menos una de las dos p o
q lo es.
De acuerdo con la definicion dada se sigue que si una de las dos, p ´o q, es verdad entonces p∨q es verdad
y que p ∨ q sera falsa, únicamente si ambas lo son.
Negación:
Dada una proposición cualquiera, p, llamaremos “negación de p” a la proposición “no p” y la notaremos
¬p. Ser´a verdadera cuando p sea falsa y falsa cuando p sea verdadera.
La tabla de verdad de esta nueva proposición, ¬p, es:
CUANTIFICADORES
Cuando se habla de cuantificadores en términos de Lógica, Teoría de Conjuntos o Matemáticas en general, se hace referencia a aquellos símbolos que se utilizan para indicar cantidad en una proposición, es decir, permiten establecer “cuántos” elementos de un conjunto determinado, cumplen con cierta propiedad.
Los cuantificadores permiten la construcción de proposiciones a partir de funciones proposicionales, bien sea particularizando o generalizando. Por ejemplo, si consideramos la función proposicional:
P(x) = x es menor que dos
Esto podría particularizarse así: “Existe un número real que es menor que dos” o generalizarlo diciendo: “Todos los números reales son menores que dos”.
En cualquiera de los dos casos, se especifica un conjunto donde está tomando valores la variable, para nuestro ejemplo, el conjunto de los números reales.
Para notar la particularización y la generalización, se utiliza la siguiente simbología, respectivamente:
Mientras que
El símbolo
Así, un cuantificador transforma una función proposicional, en una proposición a la cual se le asigna un valor de verdad.
Los cuantificadores más utilizados son entonces:
- CUANTIFICADOR UNIVERSAL
(para todo…): se utiliza para afirmar que TODOS los elementos de un conjunto, cumplen con una condición o propiedad determinada. Esto se expresa como:
- CUANTIFICADOR EXISTENCIAL
(existe al menos un…): se utiliza para indicar que existen uno o más elementos en el conjunto A que cumple(n) con una condición o propiedad determinada.
- CUANTIFICADOR EXISTENCIAL ÚNICO
(existe un único…): se utiliza para indicar que existe exactamente un elemento en el conjunto A que cumple con una condición o propiedad determinada.
Sea p(x) una función proposicional con extensión A, entonces:
Tablas de la verdad
Tabla de valores de verdad, es una tabla que despliega el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes
Existen 5 tabla de la verdad o valores de a verdad las cuales son:
La tabla del " Y" o conjunción
La tabla del " O" o disyunción
La tabla del entonces o condicional
La tabla de la equivalencia o el bicondicional
La tabla de la negación
Tabla del la conjucion
La conjunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderas
La tabla de verdad de la conjunción es la siguiente:

Tabla de la disyunción
La disyunción es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.
La tabla de verdad de la disyunción es la siguiente:
Tabla del condicional
El condicional material es un operador que opera sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad falso sólo cuando la primera proposición es verdadera y la segunda falsa, yverdadero en cualquier otro caso.
La tabla de verdad del condicional material es la siguiente:
Tabla del bicondicional
El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad difieren.
La tabla de verdad del bicondicional es la siguiente:
Tabla de la negacion:
La negación es un operador que opera. sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.





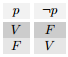



Comentarios
Publicar un comentario